Let’s imagine two scenarios: When you find someone for help, if the person says “but” with hesitation, you will probably guess that there is a 90% chance that the person will reject you. When you are at work and find your colleague who comes to work every day suddenly absence from duty, you will guess that he is sick or has something wrong at home.

Simply put, Bayes’ theorem means that our experience can correct our theory, we have to believe that there is a deviation between theory and fact and there should be a reason for abnormal things.

Now, let’s see two examples in our daily life:

1. The weather forecast predicts that the chance of rain on Wednesday and Thursday is 20% and 30% respectively, so most of the people don’t bring an umbrella with themselves. However, it rained on Wednesday. Based on your previous experience that the probability of rain for two consecutive days is 80%, you recalculate the probability of rain on Thursday, which is greater than 50%. Therefore you prepare your umbrella in advance.
2. When you are driving on the road where the intersection is ahead of you, your windshield is suddenly broken so you don’t know when to turn right. Based on your knowledge, the probability of intersections on this straight road is 5% which means you have s 95% chance to make a wrong desition to turn right. At this moment, you find a car behind your car is showing the right turn signal. Based on his experience, there is a 90% chance that the car behind him is preparing for an intersection and a 10% chance for road-side parking. Therefore, if he turns right at this moment, he’s much less likely to be wrong.

From the two examples above, We can see that using other empirical information is really helpful to determine the correctness of an action, which may significantly change theoretical forecasts and people’s subjective prediction.

Now, let’s get started to figure out how the Bayes’s theorem works. Bayes’s theorem describe the probability of an event based on the pirior probability of its related event. It can be stated mathematically as the following equation:

\(P(A \mid B) = \frac{P(B \mid A)P(A)}{P(B)}\) where A and B are events and $P(B)\neq 0$

• $P(A \mid B)$: the likelihood of event A given the likelihood of event B (prior probability)
• $P(B \mid A)$: the likelihood of event B given the likelihood of event A (posterior probability)
• $P(B)$: the likelihood of event B (marginal probability)

Considering a medical diagnosis problem, there are two possible assumptions: 1. The patient has cancer; 2. The patient doesn’t have cancer. The sample data comes from a test that also has two possible results: positive and negative. Suppose we had prior knowledge that only 0.008 of the population had the disease and that the test had a 98% chance of returning a positive result for those with the disease (true positive) and a 97% chance of returning a negative result for those without the disease (true negative).

Based on the information above, we can come up with some equations:

$P(cancer)=0.008$, $P(non-cancer)=0.992$

$P(positive \mid cacer) = 0.98$

$P(negative \mid non-cancer)=0.97$ Based on Bayes’ theorem, we can figure out the accuracy of this medical diagnosis based on our pre-knowledge. That is, we can calculate the likelihood of the patient has cancer given he has a positive result. We can build a tree to help interpretation.

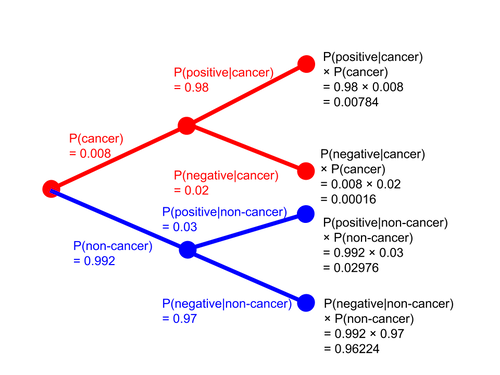
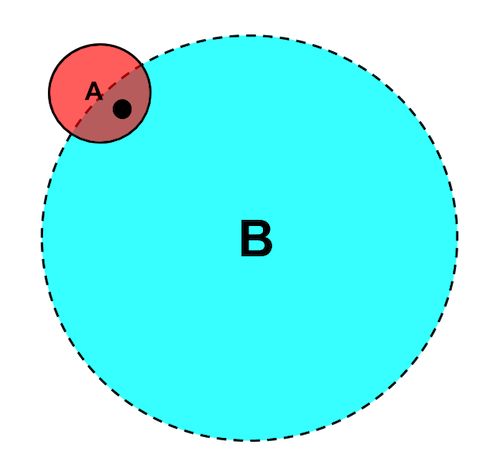
$$P(cancer \mid positive) = \frac{P(positive \mid cancer)P(cancer)}{P(positive)} = \frac{P(positive \mid cancer)P(cancer)}{P(positive \mid cancer)P(cancer)+P(positive \mid non-cancer)P(non-cancer)} = \frac{0.98 \times 0.008}{0.98 \times 0.008 + 0.03 \times 0.992} \approx 20.85 \% $$ Therefore, even if the result of medical diagnosis is positive, patients are more likely to have no cancer, which means there is a high rate of misdiagnosis. Then, let's use a Venn Diagram to understand why $P(cancer \mid positive)$ is much smaller than $P(positive \mid cancer)$. Let's suppose the likelihood of event A is much smaller than the likelihood of event B. Although we know the chance of one point falling into A is large, the chance of that point falling into B is greatly reduced.

So far, we have discussed how the Bayes' Theorem works to change theoretical probability based on empirical knowledge. High probability events may become low probability events because of other context information, and vice versa. That is the reason that I said we have to believe that there is a deviation between theory and fact and we should be curious about abnormal things to find hidden reasons. One of the most important applications of Bayes' Theorem is Bayes' inferences which enable us to make more accurate predictions according to our known evidence. The concept of Bayes' inferences has been widely used in the neural networks so that we could trackback the likelihood of hidden layers from the outcome we simulated. This algorithm has been widely used in many fields including image recognization, advertisement marketing, healthcare and stock prediction, etc. So we can say the significance of Bayes' Theorem is far beyond our imagination.